 |
 |
 |
|
|
|
|
Page 2
Courbe de Peano-Gosper
La courbe de Peano-Gosper a été découverte par R. W. Gosper . Elle est très semblable aux courbes de la page précédente. Cette courbe est "space-filling", donc de dimension fractale égale à 2. Son générateur est une figure à 7 segments qui s'inscrivent dans un triangle équilatéral.
 |
 |
 |
|
|
|
|
Courbe de Cesaro
Ces courbes sont dues à Ernest Cesaro. La courbe, dite en triangle a été tracée en 1905. Le générateur est une figure composée de 2 cotés d'un trangle isocéle, faisant un angle de 90 degrés. Sa dimension est de 2, ce qui fait qu'aprés quelques itérations, l'espace est rempli. Le générateur est tracé en alternance d'un coté ou de l'autre du segment de droite. Les trois premières courbes présentées correspondent aux niveaux 1, 2 et 8. Les 3 courbes suivantes correspondent à une légére modification du triangle de Cesaro, les 2 premiers niveaux sont identiques, mais ensuite, le générateur est tracé toujours du même coté du segment de droite.
 |
 |
 |
 |
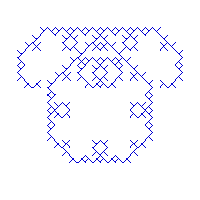 |
 |
Variation autour de la Courbe de Cesaro
Cette courbe est une variation de la courbe précédente : le générateur est composé de 2 segments de droite qui font un angle de 85 degrés au lieu de 90. Les courbes qui en résultent sont très différentes et très esthétiques.
 |
 |
 |
|
|
|
|
En vrac
Différentes Courbes
 |
 |
 |
| Cristaux de glace sur carré... | ...sur triangle |
|