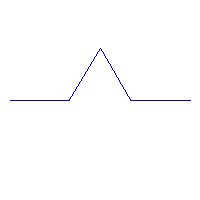
A l'origine de ce type de fractales est un générateur , une courbe plus ou moins complexe et un initiateur, qui est une figure mathématique simple : un carré, une droite, un triangle, ou un hexagone.

A la première étape, chaque segment de droite de l'initiateur est remplacé par le générateur. A l'étape suivante, chaque segment de droite de la figure obtenue à la première étape est remplacé par le générateur et ainsi de suite, jusqu'à l'infini...

En pratique, on s'arrête après une dizaine d'itérations : certaines courbes dites "space filling", ont la propriété comme leur nom l'indique, de remplir très vite toute la surface, l'initié dira que leur dimension fractale est de 2 et pour d'autres, le résultat esthétique est obtenu très vite aprés 5 ou 6 itérations.

Je vous présenterai quelque fractales, très connues, avec à chaque fois le générateur et les figures obtenues à différentes itérations.

Si la notion de dimension fractale vous intéresse, vous pouvez consulter le chapitre dimension des fractales de J.P.Louvet à Bordeaux.

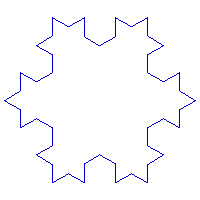
Courbe en flocon de neige

C'est la courbe la plus connue; elle est appelée courbe en flocon de neige (snowflake) et a été découverte par Helge von Koch. L'initiateur est un triangle équilatéral. B. Mandelbrot en parle dans son livre "The Fractal Geometry of Nature".

Courbe en flocon de neige

Générateur tracé sur un triangle	Etape 1	Etape 2

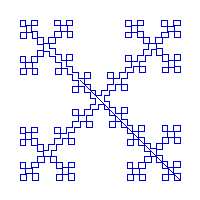
Courbe de von Koch à 5 segments

Cette courbe est une variante de la courbe précédente, la courbe en flocon de neige. L'initiateur est un carré. Bien que le générateur semble prôche de ceux présentés sur ces pages, le résultat est bien différent. Ces courbes sont ramifiées, contrairement aux courbes qui ne se coupent jamais et sont dites "self-avoiding" ou "nonramified".Les 2 courbes présentées correspondent, l'une au motif , le générateur , tracé à l'intérieur du carré, et l'autre à l'extérieur du carré. B Mandelbrot consacre un chapitre : Ramification and Fractal Lattices à ce type de courbes.

Générateur tracé sur un carré...	....à l'extérieur	....à l'intérieur

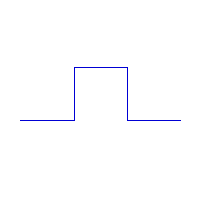
Courbes de MinKowski

Ces courbes sont attribuées au mathématicien Hermann Minkowski (1864-1904). L'initiateur est soit une droite, soit un carré. La courbe tracée sur une droite est connue sous le nom de "Minkowski Sausage". B. Mandelbrot la présente sous ce nom dans son livre "The Fractal Geometry of Nature".

Courbe de Minkowski

Générateur	Etape 2 (carré)	Minkowski Sausage-Etape3 (droite)

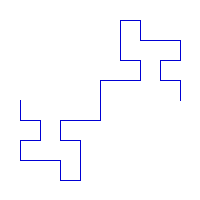
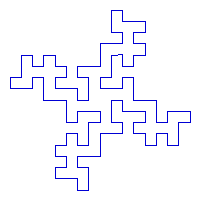
Courbe de von Koch à 32 segments

Cette courbe est très prôche des courbes précédentes, mais son générateur est plus complexe puisqu'il se compose de 32 segments. L'initiateur est un carré.

Courbe de Koch à 32 segments

Générateur tracé sur un carré	Etape 1	Etape 2

Ces courbes et celles des pages suivantes ont été tracées sur un Power Macinstosh, avec un logiciel que j'ai écrit d'aprés Roger T. Stevens et Hans Lauwerier

Ce type de fractales peut être tracé avec des programmes L-systems, conçus au départ pour étudier la croissance des plantes.

Page suivante