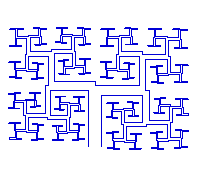Tout le monde en a vu. Elles illustrent les livres scolaires de mathématiques et elles sont partout dans la nature. Qui pensera en voyant un chou-fleur, un arbre, une plante que c'est une fractale ? et pourtant...

Fractales, si vous regardez la définition du Larousse, vous pourrez lire :

Se dit d'objets mathématiques dont la création ou la forme ne trouve ses règles que dans l'irrégularité ou la fragmentation.

Pas très claire, cette définition...

Une fractale est une figure géométrique qui consiste d'un motif qui se répète à l'infini. Faites un zoom sur une partie de fractales, puis un autre zoom, vous retrouvez le même motif. Sur l'image au dessus, vous pouvez voir un H qui se répète...

Pour celui que les mathématiques rebutent , les fractales sont avant tout des images d'une grande beauté.

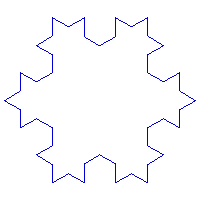
Parmi les scientifiques ayant étudié les fractales, il faut citer le français Benoît Mandelbrot. Né en 1924, en Pologne, aprés des études passées en France, B. Mandelbrot travaille quelque temps au CNRS puis il part aux Etats Unis travailler comme "IBM fellow" au centre de recherche de Watson. C'est là qu'il découvre la fameuse fractale qui porte son nom. De nombreux mathématiciens ont donné leur nom à une fractale. Parmi les noms célèbres, on trouve le suédois Helge von Koch (1870-1924) auquel on doit la courbe "flocon de neige", David Hilbert (1862-1943) et l'italien Giuseppe Peano (1858-1932) avec leur courbes "space-filling", Herman Minkowski (1864-1904), le français Gaston Julia (1893-1978), sa courbe très proche de l'ensemble de Mandelbrot est presque aussi célèbre, le polonais Waclaw Sierpinski (1882-1969) et son "gasket", Paul Lévy (1886-1971) etc...

Courbe de Péano	Flocon de neige de Von Koch
Courbe de Hilbert	Gasket de Sierpinski

Sur le site de cette université écossaise, vous trouverez les biographies de ces mathématiciens.

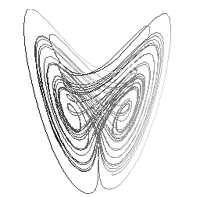
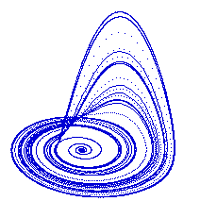
A coté de ces mathématiciens, des physiciens en résolvant les systèmes d'équations différentielles auxquels obéissent les trajectoires des corps célestes ou les trajectoires des particules élémentaires, se sont rendu compte que sous certaines conditions initiales même trés voisines, ces trajectoires devenaient imprévisibles : c'est le chaos. Pour étudier ces systèmes d'équations, ils se placent dans un espace particulier dit "espace des phases" et se sont apercus que ces trajectoires convergaient vers "un attracteur".

Beaucoup de ces physiciens ont donné leur nom aux attracteurs qu'ils ont découvert. C'est ainsi que l'on a :

• l'attracteur de Lorenz, courbe en forme d'ailes de papillons, découvert en 1963 par Edouard N. Lorenz météorologiste au M.I.T (Massachusetts Institute of Technology),
• l'attracteur de Hénon étudié vers 1976 par Michel Hénon, astronome à l'observatoire de Nice,
• l'attracteur de Rössler, découvert vers 1976 par Otto E. Rössler, spécialiste en cinétique chimique.

Mira et Gumowski au CERN à Genève ont étudié des trajectoires de particules spécialement esthétiques : de là est né le "chaos esthétique".

Attracteur de Lorenz	Attracteur de Hénon
Courbe de Mira	Attracteur de Rössler

L'attracteur de Lorenz a été créé par le logiciel "Gerry's Mandelbrot Set "de Gerry Beggs, l'attracteur de Hénon par Fractal de P. Bourke, la courbe de Mira et l'attracteur de Rössler par deux logiciels que j'ai écrits sur Power Macintosh.

Dans quelques temps, j'espère vous présenter d'autres images de ces attracteurs. En attendant, vous pouvez aller les voir, par exemple, sur le site de Paul Bourke.