Page 1

Les arbres sont des fractales, les arbres botaniques bien sur ; mais il existe aussi des arbres dans le corps humain, dans les poumons (on parle de l'arbre bronchique), et dans le système artériel.

La figure ci dessous shématise la branche d'un arbre qui se subdivise en deux branches, chacune d'elle pouvant se subdiviser à son tour en deux branches etc..

Les scientifiques ont beaucoup discuté sur cette représentation mathématique des arbres, le premier étant Léonard de Vinci. Il a écrit que le diamètre de la branche initiale est égal à la somme des diamètres des 2 branches suivantes, ces diamètres étant affectés d'un exposant alpha, appelé exposant du diamètre (relation 1). On admet que pour les arbres botaniques, alpha est égal à 2, alors que pour l'arbre bronchique, alpha doit être égal à 3, et pour le système artériel alpha doit être égal à 2,7. L'équation 2 donne la relation entre les hauteurs de deux branches successives.
Selon le choix de alpha, de la hauteur intiale L, du diamètre initial D et de l'angle fait par les 2 branches, l'aspect de l'arbre obtenu est très différent.

Voici quelques exemples d'arbres traçés de cette manière.

alpha = 3 et angle =20	alpha = 3 et angle =24	alpha = 3 et angle =20 et 38
alpha = 2 et angle =33	alpha = 2.7 et angle =33	alpha = 3 et angle =33

Un choix intéressant est celui pour lequel, le diamètre a une valeur trés faible. Les figures obtenues sont appelées "fractal canopies", mot pour lequel je ne connais pas de traduction française.

alpha = 3 et angle =10	alpha = 3 et angle =25

Un autre choix intéressant est celui pour lequel, l'angle fait par les deux branches est pris égal ou trés proche de 90°.

alpha = 2.6 et angle =90	alpha = 2.4 et angle =85

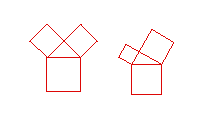
La construction des arbres suivants est plus semblable aux fractales des pages précédentes : l'arbre de Pythagore, dont le motif de base est un carré surmonté d'un triangle rectangle isocèle et de deux autres carrés plus petits, l'arbre de Pythagore "lopsided", semblable au précédent sauf que le triangle n'est pas isocéle mais a un un angle de 30°, et l'arbre de Pythagore "nu" pour lequel le carré du motif de base est réduit à une droite.

Arbre de Pythagore	Base des arbres de Pythagore	Arbre de Pythagore "lopsided"
Arbre de Mandelbrot	Arbre "réel"	Arbre de Pythagore "nu"

Sur ce sujet, on peut lire les deux chapitres consacrés aux arbres dans "The Fractal Geometry of Nature" de Benoit Mandelbrot. Je me suis inspirée aussi des livres de Roger T. Stevens et de Hans Lauwerier.